All About Asymmetric Encryption

In the previous article in this series, we looked at symmetric encryption and saw how, despite the fact that it can be a very secure form of encryption, at the end of the day we’re still talking about encryption based on the same principles as those from thousands of years ago, such as the Atbash encryption. In this type of very old-school encryption, we have two sides, A and B, that exchange information using a key which both sides have access to. If a third party somehow steals the key then communication between sides A and B has been compromised.

And yes, modern symmetric encryption makes it quite difficult to steal a key using brute force, but brute force isn’t the only way to steal a key. If sides A and B are communicating, the possibility of stealing an encryption key becomes quite real.

In light of this, let’s now turn to the RSA cryptosystem. Why RSA? The name comes from its creators. This method was developed by Ronald Rivest, Adi Shamir, and Leonard Adleman. This is a type of asymmetric encryption which means sides A and B have different keys, which is the single most important advancement in the history of cryptology.

So how does this work? In theory side A creates a public key and a private key. The public key is solely for encrypting and the private key is used solely for deciphering the encryption. Side A can publish the public key without worry or concern since it’s used solely for encrypting and not for decrypting or deciphering. Side B can take that public key, encrypt some data, and send the encrypted data to side A. Side A will then use its private key to decipher the encryption.

And how does this work? How about a little math—you guys ready? I promise it’s not going to be very difficult.

Let’s say I have a public key (5,14) and a private key (11,14). I keep the private key secret but publish the public key. Now let’s say somebody wants to send me a message—just the single digit ‘2’ is the entire message. So how would they encrypt this message? Well, they have my public key (5,14). As such, the encryption process will be as follows:

2^5mod(14)

All this is here is 2 to the 5th power, then modulus 14 (the remainder after dividing by 14). Feel free to copy this equation and paste it into Google search. Google will calculate it and return the result. Go ahead, I know you want to try it. Did you get a 4? Well, that’s the encrypted number.

The same person who encrypted their message, sends me the number 4. I take this digit and run it through my private key. It looks something like this:

4^11mod(14)

The encrypted digit, to the power of the first number of the private key and modulus of the second number. If we run this whole thing we’ll get back 2—and that my friends is the original message.

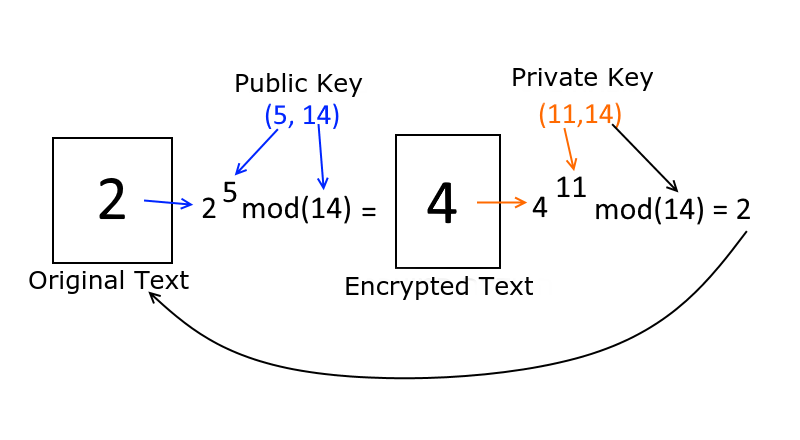
Seems pretty straight forward but the great thing is, if a third party intercepts the message, all they get is the encrypted message and the public key. The private key stays solely with the receiving party. The third party can’t do anything with what they intercepted.

Well, they can run a brute force attack and try to crack the numbers, but those numbers are so large that there’s no real way to decipher them. If you’re wondering how we calculated the public and private keys, I invite you to read the excellent article by hackernoon from where we took the example.

So that’s the theory. But how does it actually work in a real-world application, with code and everything? Let’s make an example, as always, with Node.js. And if Node isn’t your thing, just think of this example as being in pseudocode.

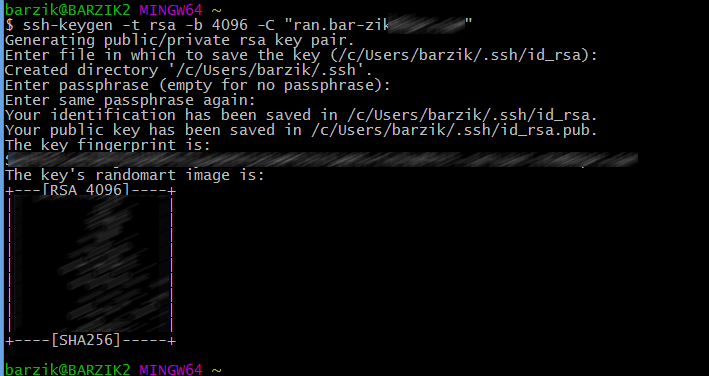
First, we need to create both a public and a private key—which is pretty easy whether you’re on Windows, Mac, or Linux. Open the terminal or the command prompt, and type:

ssh-keygen -t rsa -b 4096 -C "info@internet-israel.com" -f app/example_id_rsa

Since we’re working with Node.js, we need to convert the public key to the PEM format (which is just a different key format). This is also quite easy:

ssh-keygen -f app/example_id_rsa -e -m pem > app/example_id_rsa.pub

And now for the program itself; notice just how easy it is!

const crypto = require('crypto');

const fs = require('fs');

const path = require('path');

const RSAPath = path.resolve('./app/example_id_rsa.pub');

const RSAPrivtaePath = path.resolve('./app/example_id_rsa');

const publicKey = fs.readFileSync(RSAPath, 'utf8');

const privateKey = fs.readFileSync(RSAPrivtaePath, 'utf8');

function encrypt(text) {

   const buffer = Buffer.from(text);

   const encrypted = crypto.publicEncrypt(publicKey, buffer);

   return encrypted.toString('base64');

};

function decrypt(encryptedText) {

   const buffer = Buffer.from(encryptedText, 'base64');

   const decrypted = crypto.privateDecrypt(privateKey, buffer);

   return decrypted.toString('utf8');

};

const encryptedText = encrypt('I am super secret');

const decryptedText = decrypt(encryptedText);

console.log(encryptedText);

console.log(decryptedText);

Long story short, it’s pretty much just like symmetric encryption! It’s just that here, we’re working with two keys. The public key to encrypt the message, and the private key to decipher it. Easy peasy, lemon squeezy. We can give the public key to anyone at no risk and anyone can use it to encrypt data and send it to us. But, only those who have access to the private key have the ability to decipher that data. This is the reason why private keys must remain, well… private.

If you want to see it in action for yourself, I made a little GitHub repo where anybody can give it a whirl. Just download it, then run the keys in the console or command line. When you run it you’ll see the unencrypted and encrypted content.

That’s it for now—stay safe out there!

About the author: Ran Bar-Zik is an experienced web developer whose personal blog, Internet Israel, features articles and guides on Node.js, MongoDB, Git, SASS, jQuery, HTML 5, MySQL, and more. Translation of the original article by Aaron Raizen.